狄利克雷边界条件
狄利克雷边界条件,常微分方程的“第一类边界条件”,指定微分方程的解在边界处的值。
基本介绍
- 中文名:狄利克雷边界条件
- 外文名:Dirichlet boundary condition
- 领域:数学
- 属性:第一类边界条件”
- 作用:指定微分方程的解在边界处的值
- 相关名词:柯西边界条件
简介
在数学中,狄利克雷边界条件,为常微分方程的“第一类边界条件”,以彼得·古斯塔夫·狄利克雷(1805-1859)命名。当对一个常微分方程或偏微分方程施加时,它指定了微分方程的解在边界处的值。求出这样的方程的解的问题被称为狄利克雷问题。在套用科学中,狄利克雷边界条件也可以称为固定边界条件。
在常微分方程情况下
对于常微分方程,例如,
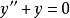
区间[a,b]的狄利克雷边界条件採取形式:
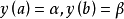
其中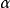 和
和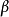 是给定的数字。
是给定的数字。
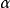
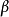
在偏微分方程情况下
对于偏微分方程,例如,
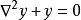
其中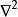 表示拉普拉斯运算元,域
表示拉普拉斯运算元,域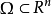 的狄利克雷边界条件採取形式:
的狄利克雷边界条件採取形式:
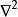
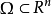
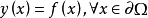
其中f是在边界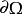 中定义的已知函式。
中定义的已知函式。
套用
例如,以下将被认为是Dirichlet边界条件:
(1)在机械工程和土木工程(梁理论)中,梁的一端保持在空间中的固定位置。
(2)在热力学中,表面保持在固定温度。
(3)在静电中,电路的节点保持固定电压。
(4)在流体动力学中,粘性流体的防滑条件表明,在固体边界处,流体相对于边界具有零速度。
其他边界条件
许多其他边界条件是可能的,包括柯西边界条件和混合边界条件。后者是狄利克雷和诺伊曼条件的组合。
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯