浮点数标準
浮点数是指一个数的小数点的位置不是固定的,而可以浮动。浮点数标準,也称IEEE二进制浮点数算术标準(IEEE 754),是20世纪80年代以来最广泛使用的浮点数运算标準,为许多CPU与浮点运算器所採用。这个标準定义了表示浮点数的格式(包括负零-0)与反常值(denormal number)),一些特殊数值(无穷(Inf)与非数值(NaN)),以及这些数值的“浮点数运算符”;它也指明了四种数值捨入规则和五种例外状况(包括例外发生的时机与处理方式)。
基本介绍
- 中文名:浮点数标準
- 外文名:Floating-point number standard
- 学科:计算机组成原理
- 别名:IEEE二进制浮点数算术标準
- 目的:规定浮点数规则以及运算细节
- 提出者:IEEE
简介
在计算机系统的发展过程中,曾经提出过多种方法表示实数,但是到为止使用最广泛的是浮点表示法。相对于定点数而言,浮点数利用指数使小数点的位置可以根据需要而上下浮动,从而可以灵活地表达更大範围的实数。 浮点数表示法利用科学计数法来表达实数。
在IEEE-754标準出现之前,业界并没有一个统一的浮点数标準,相反,很多计算机製造商都在设计自己的浮点数规则以及运算细节。
为了便于软体的移植,浮点数的表示格式应该有一个统一的标準。1985年,IEEE(Institute of Electrical and Electronics Engineers,美国电气和电子工程师协会)提出了IEEE-754标準,并以此作为浮点数表示格式的统一标準。几乎所有的计算机都支持该标準,从而大大改善了科学应用程式的可移植性。
IEEE标準从逻辑上採用一个三元组{S, E, M}来表示一个数N,它规定基数为2,符号位S用0和1分别表示正和负,尾数M用原码錶示,阶码E用移码錶示。根据浮点数的规格化方法,尾数域的最高有效位总是1,由此,该标準约定这一位不予存储,而是认为隐藏在小数点的左边,因此,尾数域所表示的值是1.M(实际存储的是M),这样可使尾数的表示範围比实际存储多一位。为了表示指数的正负,阶码E通常採用移码方式来表示,将数据的指数e 加上一个固定的偏移量后作为该数的阶码,这样做既可避免出现正负指数,又可保持数据的原有大小顺序,便于进行比较操作。
IEEE 754规定了四种表示浮点数值的方式:单精确度(32位)、双精确度(64位)、延伸单精确度(43比特以上,很少使用)与延伸双精确度(79比特以上,通常以80位实现)。只有32位模式有强制要求,其他都是选择性的。大部分程式语言都有提供IEEE浮点数格式与算术,但有些将其列为非必需的。例如,IEEE 754问世之前就有的C语言,有包括IEEE算术,但不算作强制要求(C语言的float通常是指IEEE单精确度,而double是指双精确度)。
该标準的全称为IEEE二进制浮点数算术标準(ANSI/IEEE Std 754-1985),又称IEC 60559:1989,微处理器系统的二进制浮点数算术(本来的编号是IEC 559:1989)。后来还有“与基数无关的浮点数”的“IEEE 854-1987标準”,有规定基数为2跟10的状况。最新标準是“ISO/IEC/IEEE FDIS 60559:2011”。
标準
一个浮点数 (Value) 的表示其实可以这样表示:
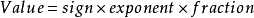
也就是浮点数的实际值,等于符号位(sign bit)乘以指数偏移值(exponent bias)再乘以分数值(fraction)。
以下是IEEE 754对浮点数格式的描述。
比特的约定
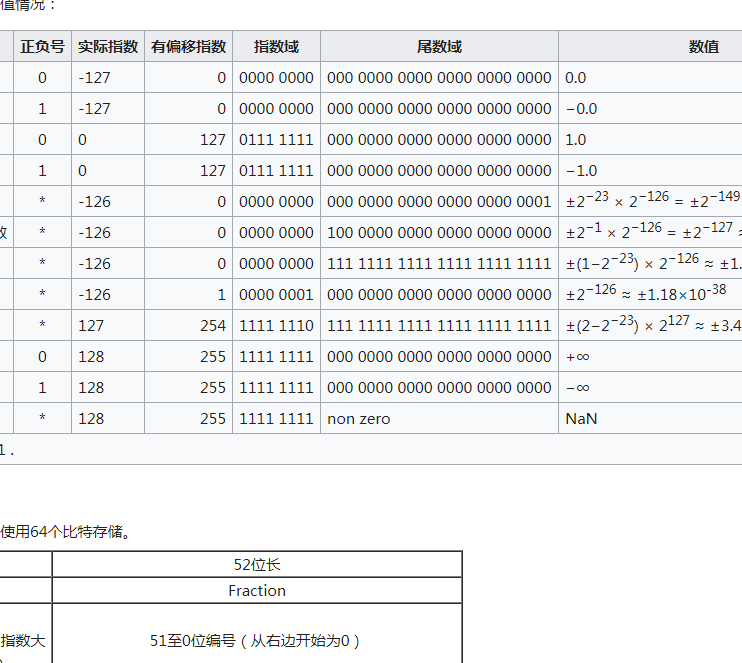
把W个比特(bit)的数据,从记忆体地址低端到高端,以0到W−1编码。通常将记忆体地址低端的比特写在最右边,称作最低有效位(Least Significant Bit,LSB),代表最小的比特,改变时对整体数值影响最小的比特。声明这一点的必要性在于X86体系架构是小端序的数据存储。对于十进制整数N,必要时表示为N10以与二进制的数的表示N2相区分。 IEEE 754浮点数的三个域
IEEE 754浮点数的三个域
 IEEE 754浮点数的三个域
IEEE 754浮点数的三个域对于一个数,其二进制科学计数法表示下的指数的值,下文称之为指数的实际值;而根据IEEE 754标準对指数部分的编码的值,称之为浮点数表示法指数域的编码值。
整体呈现
二进制浮点数是以符号数值表示法的格式存储——最高有效位被指定为符号位(sign bit);“指数部分”,即次高有效的e个比特,存储指数部分;最后剩下的f个低有效位的比特,存储“有效数”(significand)的小数部分(在非规约形式下整数部分默认为0,其他情况下一律默认为1)。
指数偏移值
指数偏移值(exponent bias),是指浮点数表示法中的指数域的编码值为指数的实际值加上某个固定的值,IEEE 754标準规定该固定值为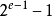 ,其中的
,其中的  为存储指数的比特的长度。
为存储指数的比特的长度。
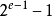

以单精度浮点数为例,它的指数域是8个比特,固定偏移值是  。此为有号数的表示方式,单精度浮点数的指数部分实际取值是从-127到128。例如指数实际值为
。此为有号数的表示方式,单精度浮点数的指数部分实际取值是从-127到128。例如指数实际值为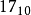 ,在单精度浮点数中的指数域编码值为
,在单精度浮点数中的指数域编码值为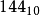 ,即
,即 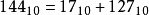 。
。

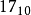
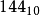
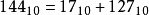
採用指数的实际值加上固定的偏移值的办法表示浮点数的指数,好处是可以用长度为 {\displaystyle e} 个比特的无符号整数来表示所有的指数取值,这使得两个浮点数的指数大小的比较更为容易,实际上可以按照字典序比较两个浮点表示的大小。这种移码錶示的指数部分,中文称作阶码。
规约形式的浮点数
如果浮点数中指数部分的编码值在 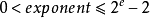 之间,且在科学表示法的表示方式下,分数 (fraction) 部分最高有效位(即整数字)是
之间,且在科学表示法的表示方式下,分数 (fraction) 部分最高有效位(即整数字)是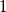 ,那幺这个浮点数将被称为规约形式的浮点数。“规约”是指用确定的浮点形式去表示一个值。由于这种表示下的尾数有一位隐含的二进制有效数字,为了与二进制科学计数法的尾数(mantissa)相区别,IEEE754称之为有效数(significant)。举例来说,双精度 (64-bit) 的规约形式浮点数在指数偏移值的值域为
,那幺这个浮点数将被称为规约形式的浮点数。“规约”是指用确定的浮点形式去表示一个值。由于这种表示下的尾数有一位隐含的二进制有效数字,为了与二进制科学计数法的尾数(mantissa)相区别,IEEE754称之为有效数(significant)。举例来说,双精度 (64-bit) 的规约形式浮点数在指数偏移值的值域为 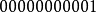 (11-bit) 到
(11-bit) 到 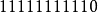 ,在分数部分则是
,在分数部分则是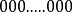 到
到 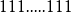 (52-bit)。
(52-bit)。
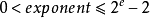
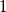
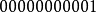
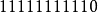
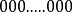
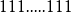
非规约形式的浮点数
如果浮点数的指数部分的编码值是0,分数部分非零,那幺这个浮点数将被称为非规约形式的浮点数。一般是某个数字相当接近零时才会使用非规约型式来表示。 IEEE 754标準规定:非规约形式的浮点数的指数偏移值比规约形式的浮点数的指数偏移值小1。例如,最小的规约形式的单精度浮点数的指数部分编码值为1,指数的实际值为-126;而非规约的单精度浮点数的指数域编码值为0,对应的指数实际值也是-126而不是-127。实际上非规约形式的浮点数仍然是有效可以使用的,只是它们的绝对值已经小于所有的规约浮点数的绝对值;即所有的非规约浮点数比规约浮点数更接近0。规约浮点数的尾数大于等于1且小于2,而非规约浮点数的尾数小于1且大于0。
除了规约浮点数,IEEE754-1985标準採用非规约浮点数,用来解决填补绝对值意义下最小规格数与零的距离。(举例说,正数下,最大的非规格数等于最小的规格数。而一个浮点数编码中,如果exponent=0,且尾数部分不为零,那幺就按照非规约浮点数来解析)非规约浮点数源于70年代末IEEE浮点数标準化专业技术委员会酝酿浮点数二进制标準时,Intel公司对渐进式下溢出(gradual underflow)的力荐。当时十分流行的DEC VAX机的浮点数表示採用了突然式下溢出(abrupt underflow)。如果没有渐进式下溢出,那幺0与绝对值最小的浮点数之间的距离(gap)将大于相邻的小浮点数之间的距离。例如单精度浮点数的绝对值最小的规约浮点数是 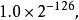 它与绝对值次小的规约浮点数之间的距离为
它与绝对值次小的规约浮点数之间的距离为 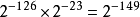 。如果不採用渐进式下溢出,那幺绝对值最小的规约浮点数与0的距离是相邻的小浮点数之间距离的
。如果不採用渐进式下溢出,那幺绝对值最小的规约浮点数与0的距离是相邻的小浮点数之间距离的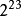 倍!可以说是非常突然的下溢出到0。这种情况的一种糟糕后果是:两个不等的小浮点数X与Y相减,结果将是0.训练有素的数值分析人员可能会适应这种限制情况,但对于普通的程式设计师就很容易陷入错误了。採用了渐进式下溢出后将不会出现这种情况。例如对于单精度浮点数,指数部分实际最小值是(-126),对应的尾数部分从
倍!可以说是非常突然的下溢出到0。这种情况的一种糟糕后果是:两个不等的小浮点数X与Y相减,结果将是0.训练有素的数值分析人员可能会适应这种限制情况,但对于普通的程式设计师就很容易陷入错误了。採用了渐进式下溢出后将不会出现这种情况。例如对于单精度浮点数,指数部分实际最小值是(-126),对应的尾数部分从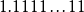 {一直到
{一直到 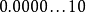 、
、 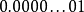 ,相邻两小浮点数之间的距离(gap)都是
,相邻两小浮点数之间的距离(gap)都是 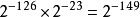 ;而与0最近的浮点数(即最小的非规约数)也是
;而与0最近的浮点数(即最小的非规约数)也是 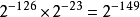 。这里有三个特殊值需要指出:
。这里有三个特殊值需要指出:
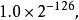
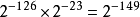
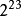
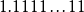
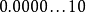
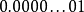
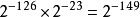
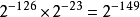
如果指数是0并且尾数的小数部分是0,这个数±0(和符号位相关);
如果指数 = 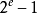 并且尾数的小数部分是0,这个数是±∞(同样和符号位相关);
并且尾数的小数部分是0,这个数是±∞(同样和符号位相关);
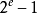
如果指数 =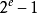 并且尾数的小数部分非0,这个数表示为不是一个数(NaN)。
并且尾数的小数部分非0,这个数表示为不是一个数(NaN)。
浮点数的比较
浮点数基本上可以按照符号位、指数域、尾数域的顺序作字典比较。显然,所有正数大于负数;正负号相同时,指数的二进制表示法更大的其浮点数值更大。
浮点数的捨入
任何有效数上的运算结果,通常都存放在较长的暂存器中,当结果被放回浮点格式时,必须将多出来的比特丢弃。 有多种方法可以用来运行捨入作业,实际上IEEE标準列出4种不同的方法:
捨入到最接近:捨入到最接近,在一样接近的情况下偶数优先(Ties To Even,这是默认的捨入方式):会将结果捨入为最接近且可以表示的值,但是当存在两个数一样接近的时候,则取其中的偶数(在二进制中式以0结尾的)。
朝+∞方向捨入:会将结果朝正无限大的方向捨入。
朝-∞方向捨入:会将结果朝负无限大的方向捨入。
朝0方向捨入:会将结果朝0的方向捨入。
浮点数的运算与函式
下述函式必须提供:
加减乘除(Add、subtract、multiply、divide)。在加减运算中负零与零相等: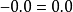
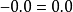
平方根(Square root):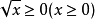 ,另规定
,另规定 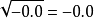 浮点余数。返回值
浮点余数。返回值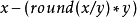 。
。
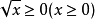
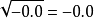
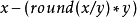
近似到最近的整数 {\displaystyle round(x)}。如果恰好在两个相邻整数之间,则近似到偶数。
比较运算. -Inf <负的规约浮点数数<负的非规约浮点数< -0.0 = 0.0 <正的非规约浮点数<正的规约浮点数< Inf;
特殊比较: -Inf = -Inf, Inf = Inf, NaN与任何浮点数(包括自身)的比较结果都为假,即 (NaN ≠ x) = false.
建议的函式与谓词
copysign(x, y): copysign(x, y)返回的值由x的不带符号的部分和y的符号组成。因此abs(x)等于copysign(x, 1.0)。copysign可以对NaN正确操作,这是少有的几个可以对NaN像普通算术一样操作有效的函式之一。C99新增了copysign函式。
−x:从涵义上指将x的符号反转。当x是±0或者NaN时,其涵义可能不同于0-x.
scalb(y, N):计算y×2N(N是整数),无需再计算2N。C99中对应的函式名是scalbn.
logb(x):计算x = 1.a×2n(x ≠ 0, a ∈[0, 1))中的n. C99新增了logb和ilogb函式。
nextafter(x,y):沿y方向找最邻近x的可表达浮点数。比如nextafter(0, 1)得到的是最小可表达的正数。C99新增了nextafter函式。
finite(x):判断x是否有限,即−Inf < x < Inf. C99新增了isfinite函式。
isnan(x):判断x是否是一个NaN,这等价于"x ≠ x". C99新增了isnan函式。
x <> y:仅当x < y或者x > y时才为True,其涵义是NOT(x = y)。注意这不同于"x ≠ y"。
unordered(x, y):当x与y无法比较大小时为True,比如说x或者y是一个NaN. C99中对应的函式名是isunordered.
class(x):区分x的浮点数类属:信号NaN、静默NaN、-Inf、负的规约浮点数,负的非规约浮点数,-0.0,0.0,正的非规约浮点数,正的规约浮点数,Inf。
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯