读书笔记摘抄新闻资讯
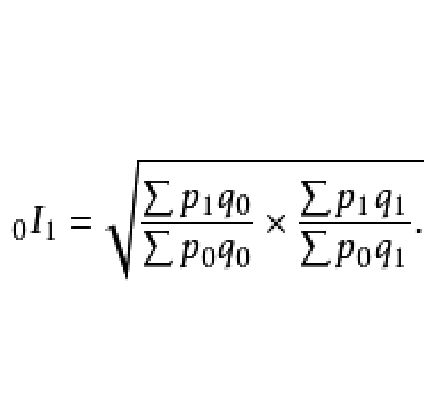
费希尔理想公式
费希尔理想公式(Fisher′s formula)是美国着名统计学家J.费希尔于1927年在其名着《统计指数的编制》中提出的主张：取拉斯贝尔斯指数和派许指数的几何平均数的一种物价指数公式。费希尔认为此公式既能满足时间颠倒测验，又能适合因子颠倒测验，所以最为理想。但此公式仍不适合循环测验。编制理想指数所需资料繁多，在实际工作中很少套用。目前，世界上只有个别国家在编制进出口商品价格指数时，套用此公式。
基本介绍
- 中文名：费希尔理想公式
- 外文名：Fisher′s formula
- 所属学科：数学（统计学）
- 提出者：J.费希尔（J.Fisher）
- 相关着作：《统计指数的编制》
- 相关概念：拉斯贝尔斯指数、派许指数等
基本介绍
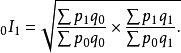
时间颠倒测验
时间颠倒测验亦称时间互换测验,指计算期对基期的指数和基期对计算期的指数的乘积应等于1。以公式表示：
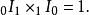
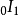
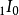
因子颠倒测验
因子颠倒测验亦称因子互换测验，指物价指数和相应的物量指数的乘积应等于其价值指数。以公式表示：
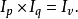
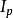
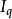
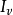
循环测验
循环测验指第一个时期对基期的指数和第二个时期对第一个时期指数的乘积，应等于第二个时期对基期的指数。以公式表示：
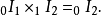
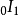
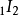
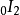
拉斯贝尔斯指数
拉斯贝尔斯指数简称拉氏指数，是指用基期的销售额作为权数，对个体价格指数求加权算术平均数，得出个综合价格指数公式；同时，用基期销售额(或产值)对个体物量指数求加权算术平均数，得出一个与价格综合指数相对应的综合物量指数的方法。这两个指数都是德国人拉斯贝尔斯于1864年提出的。拉斯贝尔斯两个综合指数的基本公式是：
拉氏价格指数公式：
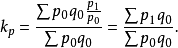
拉氏物量指数公式：
1. 以加权的综合式即得到拉氏式：
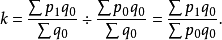
2. 以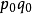
加权的算术平均式，也可得到拉氏式：
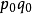
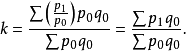
3.以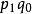
加权的调和平均式，也可得到拉氏式：
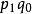
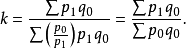
派许指数
派许指数简称派氏指数，是指用报告期的销售额作为权数，对个体价格指数求加权算术平均数，得出一个综合价格指数公式；同时；用报告期销售额对个体物量指数求加权算术平均数，得出一个与价格综合指数相对应的综合物量指数的方法，这两个指数是德国人派许于1874年提出的。派许的两个综合指数的基本公式是:
派氏价格指数公式：
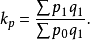
派氏物量指数公式：
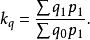
1. 以
加权的综合式，即得派氏式：
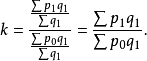
2. 以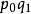
加权的算术平均式，也可得到派氏式：
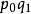
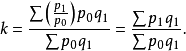
3. 以
加权的调和平均式，也可得到派氏式：
