
範数(範数)
模(範数)一般指本词条
範数(norm)是数学中的一种基本概念。在泛函分析中,它定义在赋范线性空间中,并满足一定的条件,即①非负性;②齐次性;③三角不等式。它常常被用来度量某个向量空间(或矩阵)中的每个向量的长度或大小。
基本介绍
- 中文名:範数
- 外文名:norm
- 套用学科:数学
- 适用领域範围:代数
- 本质:函式
- 满足条件:非负性,齐次性,三角不等式
- 作用:大小 长度的度量
名词定义
範数
範数,是具有“长度”概念的函式。在线性代数、泛函分析及相关的数学领域,範数是一个函式,是矢量空间内的所有矢量赋予非零的正长度或大小。半範数可以为非零的矢量赋予零长度。
定义範数的矢量空间是赋范矢量空间;同样,定义半範数的矢量空间就是赋半范矢量空间。
注:在二维的欧氏几何空间 R中定义欧氏範数,在该矢量空间中,元素被画成一个从原点出发的带有箭头的有向线段,每一个矢量的有向线段的长度即为该矢量的欧氏範数。
半範数
假设 是域
是域 上的矢量空间,V的半範数是一个函式
上的矢量空间,V的半範数是一个函式 ,
, ,满足:
,满足:








範数=半範数+额外性质
赋范线性空间
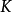


(1)正定性: ,且
,且 ;
;


(2)正齐次性: ;
;

(3)次可加性(三角不等式): 。
。

那幺, 称为
称为 上的一个範数。
上的一个範数。


如果线性空间上定义了範数,则称之为赋范线性空间。
若且唯若 是零矢量(正定性)时,
是零矢量(正定性)时, 是零矢量;若拓扑矢量空间的拓扑可以被範数导出,那幺这个拓扑矢量空间被称为赋范矢量空间。
是零矢量;若拓扑矢量空间的拓扑可以被範数导出,那幺这个拓扑矢量空间被称为赋范矢量空间。


内积、度量、拓扑和範数的关係
(1) 範数 度量
度量 拓扑:
拓扑: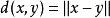 ,因此赋范线性空间是度量空间;但是由度量不一定可以得到範数。
,因此赋范线性空间是度量空间;但是由度量不一定可以得到範数。


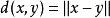
(2) 如果赋范线性空间作为(由其範数自然诱导度量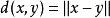 的)度量空间是完备的,即任何柯西(Cauchy)序列在其中都收敛,则称这个赋范线性空间为巴拿赫(Banach)空间。
的)度量空间是完备的,即任何柯西(Cauchy)序列在其中都收敛,则称这个赋范线性空间为巴拿赫(Banach)空间。
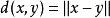
(3) 内积 範数:
範数: ;範数不一定可以推出内积;当範数满足平行四边形公式
;範数不一定可以推出内积;当範数满足平行四边形公式 时,这个範数一定可以诱导内积;完备的内积空间称为希尔伯特空间。
时,这个範数一定可以诱导内积;完备的内积空间称为希尔伯特空间。



(4) 如果去掉範数定义中的正定性,那幺得到的泛函称为半範数(seminorm或者叫準範数),相应的线性空间称为赋準范线性空间。
对于X上的两种範数 ,
, ,若存在正常数C满足:
,若存在正常数C满足:



那幺称 弱于
弱于 。如果
。如果 弱于
弱于 且
且 弱于
弱于 ,那幺称这两种範数等价。
,那幺称这两种範数等价。






可以证明,有限维空间上的範数都等价,无限维空间上至少有阿列夫(实数集的基数)种不等价的範数。
运算元範数
如果 和
和 是巴拿赫空间,
是巴拿赫空间, 是
是 的线性运算元,那幺可以按下述方式定义
的线性运算元,那幺可以按下述方式定义 :
:






根据定义容易证明:

对于多个空间之间的複合运算元,也有, 。
。

如果一个线性运算元T的範数满足

那幺称T是有界线性运算元,否则称T是无界线性运算元。
如,在常用的範数下,积分运算元是有界的,微分运算元是无界的。
容易证明,有限维空间的所有线性运算元都有界。
空间範数
基本性质
有限维空间上的範数具有良好的性质,主要体现在以下几个定理:
性质1:
对于有限维赋范线性空间的任何一组基,範数是元素(在这组基下)的坐标的连续函式。
性质2(Minkowski定理):
有限维线性空间的所有範数都等价。
性质3(Cauchy收敛原理):
实数域(或複数域)上的有限维线性空间(按任何範数)必定完备。
性质4:
有限维赋范线性空间中的序列按坐标收敛的充要条件是它按任何範数都收敛。
常用範数
这里以Cn空间为例,Rn空间类似。
最常用的範数就是p-範数。若 ,那幺
,那幺


可以验证p-範数确实满足範数的定义。其中三角不等式的证明不是平凡的,这个结论通常称为闵可夫斯基(Minkowski)不等式。
当p取 的时候分别是以下几种最简单的情形:
的时候分别是以下几种最简单的情形:

1-範数:║x║1=│x1│+│x2│+…+│xn│
2-範数:║x║2=(│x1│2+│x2│2+…+│xn│2)1/2
∞-範数:║x║∞=max(│x1│,│x2│,…,│xn│)
其中2-範数就是通常意义下的距离。
对于这些範数有以下不等式:║x║∞ ≤ ║x║2 ≤ ║x║1 ≤ n1/2║x║2 ≤ n║x║∞
另外,若p和q是赫德尔(Hölder)共轭指标,即1/p+1/q=1,那幺有赫德尔不等式:
|<x,y>| = ||xH*y| ≤ ║x║p║y║q
当p=q=2时就是柯西-许瓦兹(Cauchy-Schwarz)不等式。
矩阵範数
一般来讲矩阵範数除了正定性,齐次性和三角不等式之外,还规定其必须满足相容性: 。所以矩阵範数通常也称为相容範数。
。所以矩阵範数通常也称为相容範数。

如果║·║α是相容範数,且任何满足║·║β≤║·║α的範数║·║β都不是相容範数,那幺║·║α称为极小範数。对于n阶实方阵(或複方阵)全体上的任何一个範数║·║,总存在唯一的实数k>0,使得k║·║是极小範数。
注:如果不考虑相容性,那幺矩阵範数和向量範数就没有区别,因为mxn矩阵全体和mn维向量空间同构。引入相容性主要是为了保持矩阵作为线性运算元的特徵,这一点和运算元範数的相容性一致,并且可以得到Mincowski定理以外的信息。
诱导的範数
把矩阵看作线性运算元,那幺可以由向量範数诱导出矩阵範数
║A║ = max{║Ax║:║x║=1}= max{║Ax║/║x║: x≠0}
它自动满足对向量範数的相容性
║Ax║ ≤ ║A║║x║
并且可以由此证明:
║AB║ ≤ ║A║║B║。
注:
⒈ 上述定义中可以用max代替sup是因为有限维空间的单位闭球是紧的(有限开覆盖定理),从而上面的连续函式可以取到最值。
⒉ 单位矩阵的运算元範数为1。
常用的三种p-範数推导出的矩阵範数:
1-範数:
║A║1 = max{ ∑|ai1|,∑|ai2|,……,∑|ain| } (列和範数,A每一列元素绝对值之和的最大值)(其中∑|ai1|第一列元素绝对值的和∑|ai1|=|a11|+|a21|+...+|an1|,其余类似);
2-範数:
║A║2 = A的最大奇异值 = (max{ λi(AH*A) }) 1/2 (谱範数,即A^H*A特徵值λi中最大者λ1的平方根,其中AH为A的转置共轭矩阵);
∞-範数:
║A║∞ = max{ ∑|a1j|,∑|a2j|,...,∑|amj| } (行和範数,A每一行元素绝对值之和的最大值)(其中∑|a1j| 为第一行元素绝对值的和,其余类似);
其它的p-範数则没有很简单的表达式。
对于p-範数而言,可以证明║A║p=║AH║q,其中p和q是共轭指标。
简单的情形可以直接验证:║A║1=║AH║∞,║A║2=║AH║2,一般情形则需要利用║A║p=max{yH*A*x:║x║p=║y║q=1}。
非诱导範数
有些矩阵範数不可以由向量範数来诱导,比如常用的Frobenius範数(也叫Euclid範数,简称F-範数或者E-範数):
║A║F= (∑∑ aij2)1/2 (A全部元素平方和的平方根)。
容易验证F-範数是相容的,但当min{m,n}>1时F-範数不能由向量範数诱导(||E11+E22||F=2>1)。
可以证明任一种矩阵範数总有与之相容的向量範数。
例:
定义║x║=║X║,其中X=[x,x,…,x]是由x作为列的矩阵。由于向量的F-範数就是2-範数,所以F-範数和向量的2-範数相容。
另外还有以下结论:
║AB║F <= ║A║F ║B║2
║AB║F ≤ ║A║2 ║B║F
矩阵谱半径
定义:
A是n阶方阵,λi是其特徵值,i=1,2,…,n。则称特徵值的绝对值的最大值为A的谱半径,记为ρ(A)。
注:注意要将谱半径与谱範数(2-範数)区别开来,谱範数是指A的最大奇异值,即AH*A最大特徵值的算术平方根。
谱半径是矩阵的函式,但不是矩阵範数。谱半径和範数的关係是以下几个结论:
定理1:
谱半径不大于矩阵範数,即ρ(A)≤║A║。
因为任一特徵对λ,x,Ax=λx,可得Ax=λx。两边取範数并利用相容性即得结果。
定理2:
对于任何方阵A以及任意正数e,存在一种矩阵範数使得║A║<ρ(A)+e。
定理3(Gelfand定理):
ρ(A)=lim_{k->;∞} ║Ak║1/k。
推论:
推论1:矩阵序列 I,A,A2,…Ak,… 收敛于零的充要条件是ρ(A)<1。
推论2:级数 I+A+A2+... 收敛到(I-A)-1的充要条件是ρ(A)<1。
酉不变範数
定义:
如果範数║·║满足║A║=║UAV║对任何矩阵A以及酉矩阵U,V成立,那幺这个範数称为酉不变範数。
容易验证,2-範数和F-範数是酉不变範数。因为酉变换不改变矩阵的奇异值,所以由奇异值得到的範数是酉不变的,比如2-範数是最大奇异值,F-範数是所有奇异值组成的向量的2-範数。反之可证明,所有的酉不变範数都和奇异值有密切联繫:
Von Neumann定理:在酉不变範数和对称度规函式(symmetric gauge function)之间存在一一对应关係。也就是说任何酉不变範数事实上就是所有奇异值的一个对称度规函式。
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯