
支付矩阵
支付矩阵,也称“赢得矩阵”、报酬矩阵、收益矩阵、得益矩阵,是指从支付表中抽象出来由损益值形成的矩阵,用来描述两个人或多个参与人的策略和支付的矩阵。不同参与人的利润或效用就是支付。在实验心理学的信号检测论中,指在一定的信号和噪音出现的先定机率条件下,对被试判断结果的奖惩办法。
基本介绍
- 中文名:支付矩阵
- 外文名:Payoff matrix
- 领域:运筹学
- 属性:由损益值组成的矩阵
- 别称:赢得矩阵、得益矩阵等
- 相关名词:收益矩阵
关係介绍
支付矩阵 (pay-off matrix)是包含备择行动方案、自然状态和损益值(或效用值)的矩阵。备择行动方案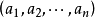 是满足决策目标的n个可行的备择方案。它们彼此独立。所有方案的集合A:{a}称为行动空间或决策空间。自然状态
是满足决策目标的n个可行的备择方案。它们彼此独立。所有方案的集合A:{a}称为行动空间或决策空间。自然状态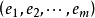 是各种行动方案可能遇到的状态。它们往往是随机的,可以用机率
是各种行动方案可能遇到的状态。它们往往是随机的,可以用机率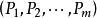 表示。所有状态的集合E:{e}称为状态空间。各自然状态出现的机率P建立在主观观测与经验估算的基础上,为主观机率。所有机率及其状态构成机率空间。对应于
表示。所有状态的集合E:{e}称为状态空间。各自然状态出现的机率P建立在主观观测与经验估算的基础上,为主观机率。所有机率及其状态构成机率空间。对应于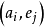 的损益值(或支付值),是行动方案
的损益值(或支付值),是行动方案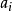 在自然状态e条件下所产生的收益值(正值)或损失值(负值),其集合为
在自然状态e条件下所产生的收益值(正值)或损失值(负值),其集合为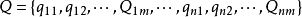 效用值域为
效用值域为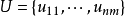 、其中
、其中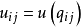 。
。
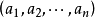
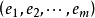
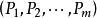
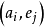
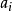
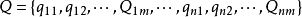
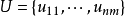
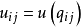
经济意义
在价格战中,企业和竞争者之间是一种非合作博弈关係。在博弈过程中,企业和竞争者都有两种策略选择:降价和不降价。假定在某一产业中形成了寡头市场结构,有两个企业A和B生产同一类产品。他们共同分享同一市场,在降价前各自获得的收益相等均为R;当採取价格战时,一个企业认为先通过降价可以获得较高的市场份额,由此可使得收益增加为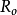 ,相对于另一个企业不降价因此而损失
,相对于另一个企业不降价因此而损失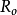 的收益:如果另一个企业也同样採取降价策略,那幺面对既定的市场,两个企业会因价格下降而带来损失,损失都为
的收益:如果另一个企业也同样採取降价策略,那幺面对既定的市场,两个企业会因价格下降而带来损失,损失都为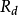 (且
(且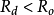 )。这样就形成了下表的博弈支付矩阵:
)。这样就形成了下表的博弈支付矩阵:
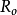
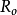
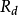
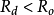

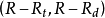
继续採用上面的假设,现在来分析下面情况,既然双方降价与谁都无利,那幺当一个降价,另一个不降价而採用其他价格竞争策略(比如搞好售后服务等)时,会出现不同情况,由于採用某种策略适应了社会需求,受到消费者的普遍赞同,从而吸引了大量的顾客,会产生新的收益分配的格局,形成了下面的支付矩阵:

该支付矩阵儘管是将表一中右上角和左下角对调,但却有着不同的经济含义和博弈后果。同样可以得到:不管B採取降价与不降价策略,A都会採取不降价策略:而对于B而言,也会是同样的抉择。因此,(不降价,不降价)变成了该支付矩阵的纳什均衡。这样,双方达成了一种默契和共识——合作。
通过上面的分析不难看出,採取合作的态度比起双方採用降价竞争的策略有利多了,显然是一种较为良性的状态。但它并非是理想的均衡状态,如果仅仅是维持现状,满足现存的收益水平,那幺整个行业乃至社会将不思进取,也将不会有经济社会的繁荣。
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯