读书笔记摘抄新闻资讯
公切线
公切线是指同时相切于两条或两条以上的曲线的直线，例如和两个圆相切的直线叫做这两个圆的公切线。如果两个圆在公切线的同侧，则这公切线叫外公切线；如果两个圆在公切线的异侧，则叫内公切线。
基本介绍
- 中文名：公切线
- 外文名：common tangent
- 定义：相切于两条，两条以上曲线的直线
- 分类：外公切线，内公切线
- 研究领域：数学
公切线性质
1.两圆的两条外公切线长相等；
2.两条内公切线的长也相等。
3.两圆的外公切线与连心线或者交于一点或者平行。
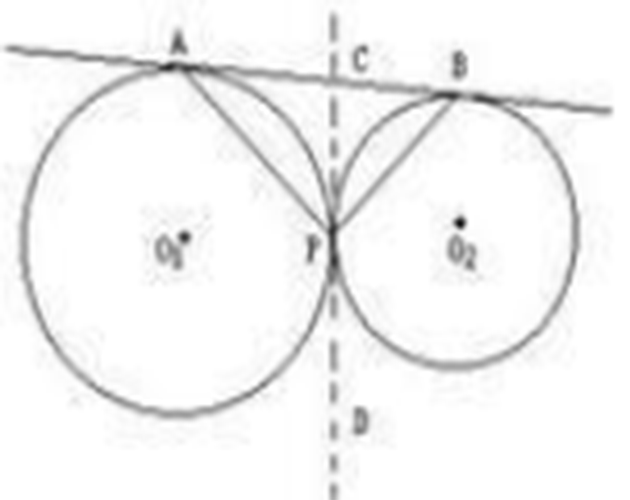
两圆的外公切线如图1所示。
图1两圆的外公切线数量关係
外公切线的长=根号下圆心距的平方-大圆半径减小圆半径的平方=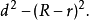
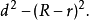
内公切线的长=根号下圆心距的平方-大圆半径加小圆半径的平方=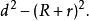
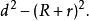
外公切线与连心线夹角的正弦值=圆心距分之大圆半径减小圆半径；
内公切线与连心线夹角的正弦值=圆心距分之大圆半径加小圆半径。
位置关係
公切线的条数与两圆的位置关係如下：
若两圆相离，则有4条公切线；
若两圆外切，则有3条公切线（两外切，一内切）；
两圆相交，则有2条公切线（外切）；
若两圆内切，则有1条公切线；
若两圆内含，则有0条公切线。
尺规作图方法
方法一：平移法（如图2所示）
- 取圆O1，圆O2上的半径O1A，O2B；
- 以B为圆心，以O1A的长度为半径画圆交O2B于C；
- 以为O1O2直径画圆D，以O2为圆心，O2C的长度为半径画圆，与圆D交与E；
- 连线O2E并延长交圆O2于F；
- 过O1作O1G||O2F交圆G，则直线GF即为所求。
图2 平移法方法二：位似法（如图3所示）
- 作圆O1的一条半径O1A，在圆O2中取一条与之平行的半径O2B；
- 连线BA，O2O1并延长交于P；
- 取PO1中点C，以C为圆心，CP长为半径画弧交圆O1于D，作直线PD，那幺直线PD也与圆O1、圆O2相切。
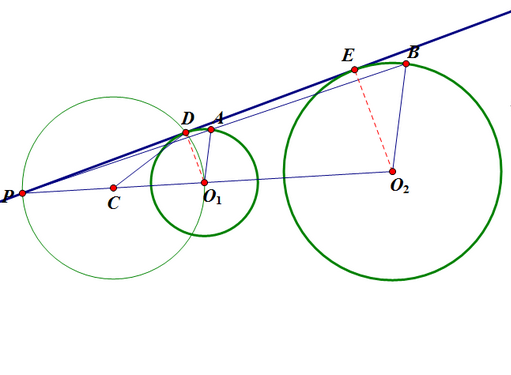图3 位似法例题
作外公切线
已知：圆O半径为R，O'半径为r（假设R>r），求作它们的外公切线。
作法：
- 连线OO'，作出线段OO'的中点M；
- 以M为圆心，MO为半径画圆；
- 以O为圆心，R-r为半径画圆，与圆M的交点记作A、A'；
- 作射线OA交圆O于Q，过O'作OQ的平行线，交圆O'于P；
- 过P、Q作直线，直线PQ即为所求（如图4所示）。
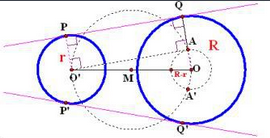图4 作外公切线作内公切线
- 连OO'，作出线段OO'的中点M；
- 以M为圆心，MO为半径画圆
- 以O为圆心，R+r为半径画圆，与圆M的交点记作A，A'；
- 作射线OA交圆O于Q，过O'作OQ的平行线，交圆O'于P；
- 过P、Q作直线，直线PQ即为所求（如图5所示）。
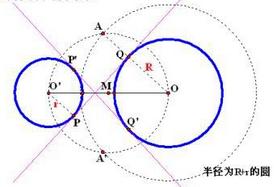图5 内公切线