热膨胀分析
热膨胀分析即是从测量金属在温度改变时或相变尺寸效应的变化来研究金属内部的转变,可以用来测定金属在加热与冷却过程中的临界点及热膨胀係数等,并广泛地用于研究钢在淬火与回火状态的各种变化。
基本介绍
- 中文名:热膨胀分析
- 内容:研究金属内部的转变
- 要求:测定金属在加热与冷却的临界点
- 类型:物理
分析原理
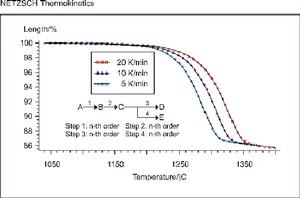
物体因温度改变而发生的膨胀现象叫“热膨胀”。通常是指外压强不变的情况下,大多数物质在温度升高时,其体积增大,温度降低时体积缩小。在相同条件下,气体膨胀最大,液体膨胀次之,固体膨胀最小。也有少数物质在一定的温度範围内,温度升高时,其体积反而减小。因为物体温度升高时,分子运动的平均动能增大,分子间的距离也增大,物体的体积随之而扩大;温度降低,物体冷却时分子的平均动能变小,使分子间距离缩短,于是物体的体积就要缩小。又由于固体、液体和气体分子运动的平均动能大小不同,因而从热膨胀的巨观现象来看亦有显着的区别。
热膨胀係数
物体由于温度改变而有胀缩现象。其变化能力以等压(p一定)下,单位温度变化所导致的体积变化,即热膨胀係数表示热膨胀係数α=ΔV/(V*ΔT),式中ΔV为所给温度变化ΔT下物体体积的改变,V为物体体积。
严格说来,上式只是温度变化範围不大时的微分定义式的差分近似;準确定义要求ΔV与ΔT无限微小,这也意味着,
严格说来,上式只是温度变化範围不大时的微分定义式的差分近似;準确定义要求ΔV与ΔT无限微小,这也意味着,

热膨胀係数在较大的温度区间内通常不是常量。温度变化不是很大时,α就成了常量,利用它,可以把固体和液体体积膨胀表示如下:
Vt=V0(1+3αΔT),
而对理想气体,Vt=V0(1+0.00367ΔT);Vt、V0分别为物体末态和初态的体积。
对于可近似看做一维的物体,长度就是衡量其体积的决定因素,这时的热膨胀係数可简化定义为:单位温度改变下长度的增加量与的原长度的比值,这就是线膨胀係数。
对于三维的具有各向异性的物质,有线膨胀係数和体膨胀係数之分。如石墨结构具有显着的各向异性,因而石墨纤维线膨胀係数也呈现出各向异性,表现为平行于层面方向的热膨胀係数远小于垂直于层面方向。
巨观热膨胀係数与各轴向膨胀係数的关係式有多个,普遍认可的有Mrozowski算式:α=Aαc+(1-A)αa
αc,αa分别为a轴和c轴方向的热膨胀率,A被称为“结构端面”参数。
Vt=V0(1+3αΔT),
而对理想气体,Vt=V0(1+0.00367ΔT);Vt、V0分别为物体末态和初态的体积。
对于可近似看做一维的物体,长度就是衡量其体积的决定因素,这时的热膨胀係数可简化定义为:单位温度改变下长度的增加量与的原长度的比值,这就是线膨胀係数。
对于三维的具有各向异性的物质,有线膨胀係数和体膨胀係数之分。如石墨结构具有显着的各向异性,因而石墨纤维线膨胀係数也呈现出各向异性,表现为平行于层面方向的热膨胀係数远小于垂直于层面方向。
巨观热膨胀係数与各轴向膨胀係数的关係式有多个,普遍认可的有Mrozowski算式:α=Aαc+(1-A)αa
αc,αa分别为a轴和c轴方向的热膨胀率,A被称为“结构端面”参数。
分析对象
膨胀係数:为表征物体受热时,其长度、面积、体积变化的程度,而引入的物理量。它是线膨胀係数、面膨胀係数和体膨胀係数的总称。
固体热膨胀:固体热膨胀现象,从微观的观点来分析,它是由于固体中相邻粒子间的平均距离随温度的升高而增大引起的。晶体中两相邻粒子间的势能是它们中心距离的函式,根据这种函式关係所描绘的曲线,如图2-6所示,称为势能曲线。它是一条非对称曲线。在一定温度下,粒子在平衡位置附近振动、具有的动能为EK,总能量为EK与相互作用能EP之和,它在整个运动过程中是守恆的。图中,粒子间最接近的距离是r′,最远的距离是r〃。由于距离减小所引起的斥力增长比由于距离增大所引起的引力下降快的多,因而粒子间接近的距离与粒子间远离的距离关係是 r0r′<r〃-r0所以两相邻粒子中心的平均距离为 变的情形。由此可见,当晶体温度升高,粒子热振动加剧,体积膨胀。
固体的线膨胀:由于固体随温度的变化而变化,当温度变化不太大时,在某一方向长度的改变数称为“固体的线膨胀”。例如,一细金属棒受热而伸长。固体的任何线度,例如,长度、宽度、厚度或直径等,凡受温度影响而变化的,都称之为“线膨胀”。
线膨胀係数:亦称线胀係数。固体物质的温度每改变1摄氏度时,其长度的变化和它在0℃时长度之比,叫做“线膨胀係数”。单位为1/开。符号为αl。其定义式是 即有lt=l0(l+αlt)。由于物质的不同,线膨胀係数亦不相同,其数值也与实际温度和确定长度l时所选定的参考温度有关,但由于固体的线膨胀係数变化不大,通常可忽略这种变化,而将α当作与温度无关的常数。
固体的面膨胀:当固体的温度变化不大时,其表面积随温度的升高而增大,这一现象叫“固体的面膨胀”。遵循的规律为:St=S0(1+αst)式中αs为面膨胀係数,单位是1/开,其量值为αs≈2ατ。
固体的体膨胀:当固体的温度变化不大时,其体积随温度的升高而增大,这一现象叫“固体的体膨胀”。
固体热膨胀:固体热膨胀现象,从微观的观点来分析,它是由于固体中相邻粒子间的平均距离随温度的升高而增大引起的。晶体中两相邻粒子间的势能是它们中心距离的函式,根据这种函式关係所描绘的曲线,如图2-6所示,称为势能曲线。它是一条非对称曲线。在一定温度下,粒子在平衡位置附近振动、具有的动能为EK,总能量为EK与相互作用能EP之和,它在整个运动过程中是守恆的。图中,粒子间最接近的距离是r′,最远的距离是r〃。由于距离减小所引起的斥力增长比由于距离增大所引起的引力下降快的多,因而粒子间接近的距离与粒子间远离的距离关係是 r0r′<r〃-r0所以两相邻粒子中心的平均距离为 变的情形。由此可见,当晶体温度升高,粒子热振动加剧,体积膨胀。
固体的线膨胀:由于固体随温度的变化而变化,当温度变化不太大时,在某一方向长度的改变数称为“固体的线膨胀”。例如,一细金属棒受热而伸长。固体的任何线度,例如,长度、宽度、厚度或直径等,凡受温度影响而变化的,都称之为“线膨胀”。
线膨胀係数:亦称线胀係数。固体物质的温度每改变1摄氏度时,其长度的变化和它在0℃时长度之比,叫做“线膨胀係数”。单位为1/开。符号为αl。其定义式是 即有lt=l0(l+αlt)。由于物质的不同,线膨胀係数亦不相同,其数值也与实际温度和确定长度l时所选定的参考温度有关,但由于固体的线膨胀係数变化不大,通常可忽略这种变化,而将α当作与温度无关的常数。
固体的面膨胀:当固体的温度变化不大时,其表面积随温度的升高而增大,这一现象叫“固体的面膨胀”。遵循的规律为:St=S0(1+αst)式中αs为面膨胀係数,单位是1/开,其量值为αs≈2ατ。
固体的体膨胀:当固体的温度变化不大时,其体积随温度的升高而增大,这一现象叫“固体的体膨胀”。

体积膨胀係数:或称“体胀係数”。无论物质是哪种(固体、液体或气体)形态的变化,都称之为体膨胀。当物体温度改变1摄氏度时,其体积的变化和它在0℃时体积之比,叫做“体积膨胀係数”。符号用α表示。设在0℃时物质的体积为V0,在t℃时的体积为Vt,则体胀係数的定义式为 即有Vt=V0(1+αt)。由于固体或液体的膨胀係数很小,为计算方便起见,在温度不甚高时,可直接用下式计算,无需再求0℃时的体积V0V2=V1[1+α(t2-t1)]。式中V1是在t1℃时的体积,V2是在t2℃时的体积。这一式只适用于固体或液体,因为气体物质的膨胀係数值较大,不能运用此式。
液体热膨胀:液体是流体,因而只有一定的体积,而没有一定的形状。它的体膨胀遵循Vt=V0(1+βt)的规律,β是液体的体膨胀係数。其膨胀係数,一般情况是比固体大得多。
气体的热膨胀:气体热膨胀的规律较複杂,当一定质量气体的体积,受温度影响上升变化时,它的压强也可能发生变化。若保持压强不变,则一定质量的气体,必然遵循着Vt=V0(1+γt)的规律,式中的γ是气体的体膨胀係数。盖·吕萨克定律,反映了气体体积随温度变化的规律。这一定律也可表述为:一定质量的气体,在压强不变的情况下,温度每升高(或降低)1℃,增加(或减小)的体积等于它在0℃时体积。
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯