读书笔记摘抄新闻资讯特纳定理
特纳定理是关于共线点的一个定理。若P，Q是关于△ABC外接圆的一对反演点，点P关于BC，CA，AB三边的对称点分别为U，V，W，且QU，QV，QW和边BC，CA，AB或其延长线的交点分别为D，E，F，则D，E，F在同一直线上。
基本介绍
- 中文名：特纳定理
- 外文名：Turner theorem
- 适用範围：数理科学
简介
特纳定理是关于共线点的一个定理。
若P，Q是关于△ABC外接圆的一对反演点，点P关于BC，CA，AB三边的对称点分别为U，V，W，且QU，QV，QW和边BC，CA，AB或其延长线的交点分别为D，E，F，则D，E，F在同一直线上（如图）。
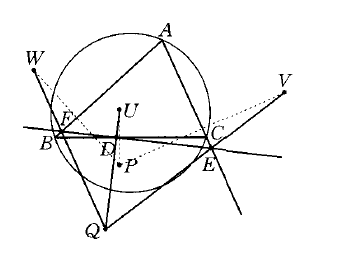图1帕斯卡定理
帕斯卡定理是一个着名的共线点定理，指圆锥曲线内接六边形（包括退化的六边形）其三对边的交点共线，与布列安桑定理对偶，是帕普斯定理的推广。
定理约于公元1639年为法国数学家布莱士·帕斯卡(Blaise Pascal)所发现，被称为帕斯卡定理，是射影几何中的一个重要定理。
阿里加定理
(Ariga theorem)
阿里加定理是关于共点线的一个定理。
若P为△ABC外接圆上的一点，l1为点P关于△ABC的西姆森线，QR为△ABC的外接圆的弦，且QR⊥l1，又l2，l3分别为点R，Q关于△ABC的西姆森线，则l1，l2，l3交于一点（如图）。
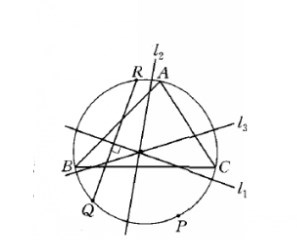图2