一致绝对收敛
绝对收敛是数学中无穷级数和广义积分的一种性质。一个数项级数或一个积分绝对收敛若且唯若级数的每一项或者积分的函式取绝对值(或範数)后仍然收敛或可积。
基本介绍
- 中文名:一致绝对收敛
- 领域:数学
介绍
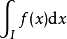
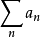
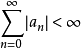
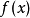
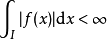
在无穷级数的研究中,绝对收敛性是一项足够强的条件,许多有限项级数具有的性质,在一般的无穷级数不一定满足,只有在绝对收敛的无穷级数也会具有该性质。例如任意重排一个绝对收敛的级数之通项的次序,不会改变级数的和,又如,两个绝对收敛的无穷级数通项的乘积以任何方式排列成的级数和都为原来两个级数和的乘积。收敛但不是绝对收敛的无穷级数或积分被称为条件收敛的。
定义
绝对收敛是建立在实数绝对值、複数的模长以及更一般的,向量的範数概念之上的。绝对值、模长都是範数概念的特例。给定一个向量空间V,範数 是将V中元素映射到非负实数上的一个函式,并且满足以下性质:
是将V中元素映射到非负实数上的一个函式,并且满足以下性质:

将且仅将零向量映射到0: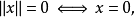
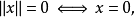
齐次性: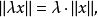
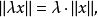
次可加性: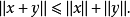
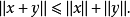
装备了範数的向量空间V被称为赋范向量空间,可以定义距离: 这样可以定义V上的拓扑结构,从而定义收敛乃至绝对收敛。设有由V中元素组成的级数:
这样可以定义V上的拓扑结构,从而定义收敛乃至绝对收敛。设有由V中元素组成的级数: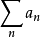 ,则此级数绝对收敛若且唯若由每一项向量的範数构成的正项级数
,则此级数绝对收敛若且唯若由每一项向量的範数构成的正项级数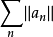 收敛:
收敛:

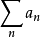
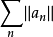

当级数的每一项是实数或複数时,对应的是实向量空间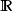 和复向量空间
和复向量空间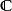 ,这时对应的範数是实数的绝对值和複数的模长,都写作
,这时对应的範数是实数的绝对值和複数的模长,都写作 ,所以实数项或複数项的级数绝对收敛,若且唯若由每一项元素的绝对值或模长构成的正项级数
,所以实数项或複数项的级数绝对收敛,若且唯若由每一项元素的绝对值或模长构成的正项级数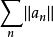 收敛:
收敛:

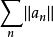
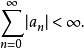
 读书笔记摘抄新闻资讯
读书笔记摘抄新闻资讯